Overview

NUBO, short for Newcastle University Bayesian optimisation, is a Bayesian optimisation framework for the optimisation of expensive-to-evaluate black-box functions, such as physical experiments and computer simulations. It is developed and maintained by the Fluid Dynamics Lab at Newcastle University. NUBO focuses primarily on transparency and user experience to make Bayesian optimisation easily accessible to researchers from all disciplines. Transparency is ensured by clean and comprehensible code, precise references, and thorough documentation. User experience is ensured by a modular and flexible design, easy-to-write syntax, and careful selection of Bayesian optimisation algorithms. NUBO allows you to tailor Bayesian optimisation to your specific problem by writing the optimisation loop yourself using the provided building blocks or using an off-the-shelf algorithm for common problems. Only algorithms and methods that are sufficiently tested and validated to perform well are included in NUBO. This ensures that the package remains compact and does not overwhelm the user with an unnecessarily large number of options. The package is written in Python but does not require expert knowledge of Python to optimise your simulations and experiments. NUBO is distributed as open-source software under the BSD 3-Clause licence.

Contact

Thanks for considering NUBO. If you have any questions, comments, or issues feel free to email us at m.diessner2@newcastle.ac.uk. Any feedback is highly appreciated and will help make NUBO better in the future.

Bayesian optimisation

Bayesian optimisation [1] [3] [4] [9] [10] is a surrogate model-based optimisation algorithm that aims to maximise an objective function in a minimum number of function evaluations. The underlying mathematical expression of the objective function is usually unknown or non-existent and every function evaluation is expensive. Solving such a function requires a cost-effective and sample-efficient optimisation strategy. Bayesian optimisation fulfils these criteria by representing the objective function through a surrogate model, often a Gaussian process [3] [13]. This representation can be used to find the next point that should be evaluated by maximising a criterion specified through an acquisition function. A popular criterion is, for example, the expected improvement (EI) [4], which is the expectation that the new point returns a better solution than the current best point. Bayesian optimisation is performed in a loop where training data is used to fit the surrogate model before the next point suggested by the acquisition function is evaluated and added to the training data. The loop restarts and gathers more information about the objective function with each iteration. Bayesian optimisation is run for as many iterations as the evaluation budget allows, until a satisfactory solution is found, or until a predefined stopping criterion is met.

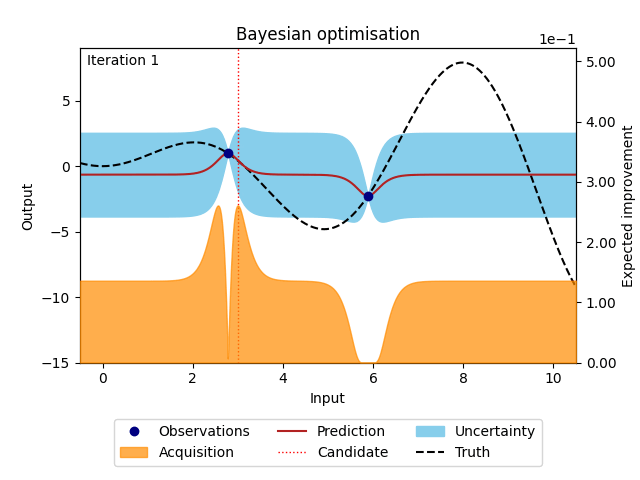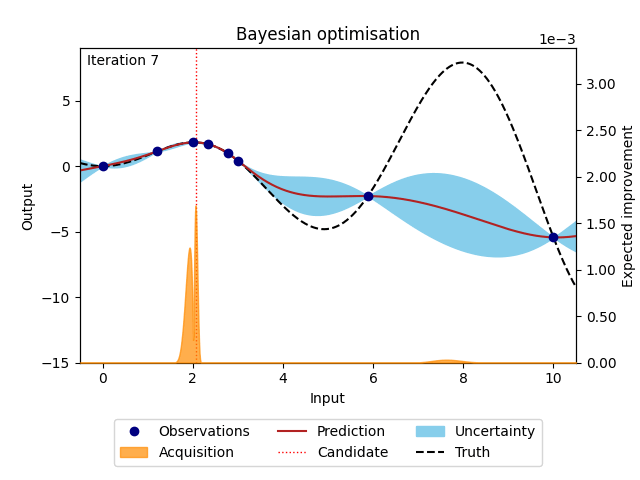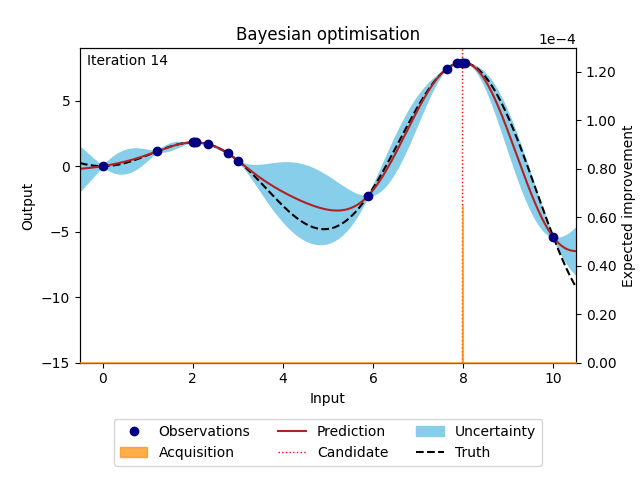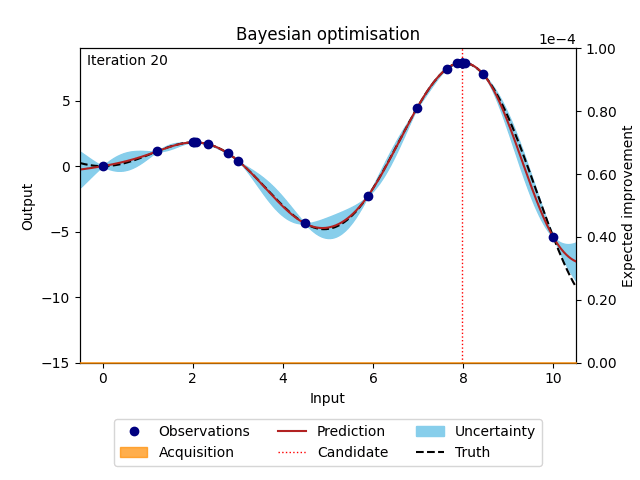
Figure 1: Bayesian optimisation of a 1D toy function with a budget of 20 evaluations.

Contents

Algorithms

NUBO provides some off-the-shelf optimisation algorithms that can solve typically black-box functions. For more complex problem, custom optimiasation loops might be necessary.

Surrogate models

NUBO focuses on the use of Gaussian Processes as surrogates for the objective function. Gaussian Processes [3] [13] are specified through the GPyTorch package [2], a powerful package that allows the implementation of a wide selection of models ranging from exact Gaussian processes to approximate and even deep Gaussian processes. Hyper-parameters can be estimated via maximum likelihood estimation (MLE), maximum a posteriori estimation (MAP) or fully Bayesian estimation.

Acquisition functions

NUBO supports the use of analytical acquisition functions and approximations through Monte Carlo sampling. Analytical expected improvement (EI) [4] and upper confidence bound (UCB) [12] can be used for sequential single-point problems where results are evaluated after each iteration. Multi-point batches for parallel evaluation or asynchronous problems, where the optimisation algorithm is continued while other points are still being evaluated, can be performed via Monte Carlo acquisition functions [14].

Optimisers

The deterministic analytical acquisition functions are optimised via multi-start L-BFGS-B [15] if the input space is restricted by box bounds or multi-start SLSQP [6] if the input space is also restricted by constraints. The stochastic Monte Carlo acquisition functions that are based on random samples are maximised with the stochastic optimiser Adam [5]. NUBO also supports the optimisation of mixed parameter space (continuous and discrete).

Design of experiments

Initial training data points can be generated with space-filling designs. NUBO supports random or maximin Latin hypercube designs [7].

Synthetic test functions

NUBO provides ten synthetic test functions that allow the validation of Bayesian optimisation algorithms before applying them to expensive experiments [11].

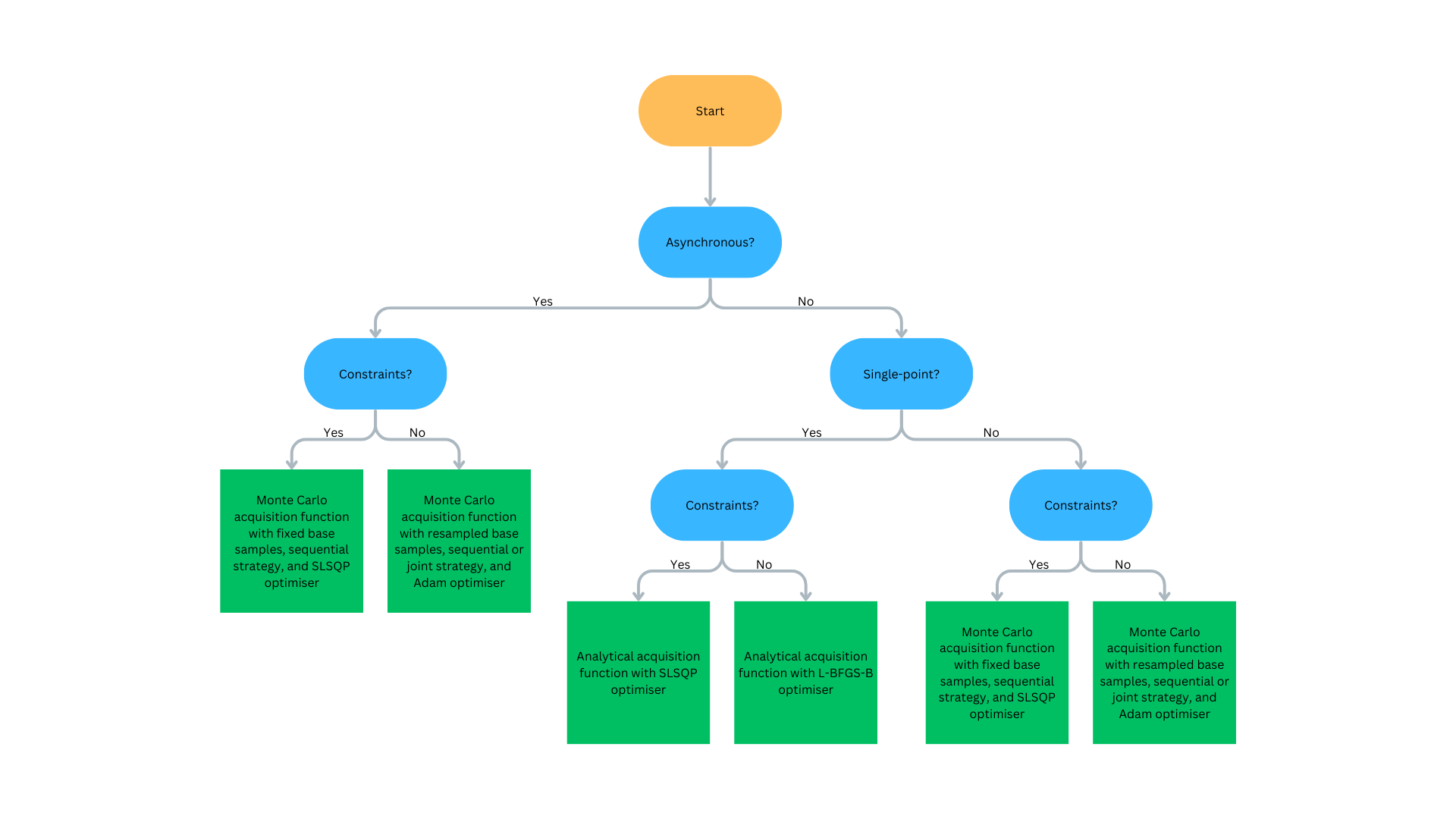
Figure 2: Flowchart to determine what Bayesian optimisation algorithm is recommended. Click to expand.

---

[1]

PI Frazier, “A Tutorial on Bayesian Optimization,” arXiv preprint arXiv:1807.02811, 2018.

[2]

J Gardner, G Pleiss, KQ Weinberger, D Bindel, and AG Wilson, “GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with Gpu Acceleration,” Advances in Neural Information Processing Systems, vol. 31, 2018.

[3] (1,2,3)

RB Gramacy, Surrogates: Gaussian Process Modeling, Design, and Optimization for the Applied Sciences, 1st ed. Boca Raton, FL: CRC press, 2020.

[4] (1,2,3)

DR Jones, M Schonlau, and WJ Welch, “Efficient Global Optimization of Expensive Black-Box Functions,” Journal of Global Optimization, vol. 13, no. 4, p. 566, 1998.

[5]

DP Kingma and J Ba, “Adam: A Method for Stochastic Optimization,” Proceedings of the 3rd International Conference on Learning Representations, 2015.

[6]

D Kraft, “Algorithm 733: TOMP-Fortran Modules for Optimal Control Calculations,” ACM Transactions on Mathematical Software (TOMS), vol. 20, no. 3, p. 262-281, 1994.

[7]

MD McKay, RJ Beckman, and WJ Conover, “A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code,” Technometrics, vol. 42, no. 1, p. 55-61, 2000.

[8]

J O’Connor, M Diessner, KJ Wilson, RD Whalley, A Wynn, and S Laizet, “Optimisation and Analysis of Streamwise-Varying Wall-Normal Blowing in a Turbulent Boundary Layer,” Flow, Turbulence and Combustion, 2023.

[9]

B Shahriari, K Swersky, Z Wang, RP Adams, and N De Freitas, “Taking the Human Out of the Loop: A Review of Bayesian Optimization,” Proceedings of the IEEE, vol. 104, no. 1, p. 148-175, 2015.

[10]

J Snoek, H Larochelle, and RP Adams, “Practical Bayesian Optimization of Machine Learning Algorithms,” Advances in Neural Information Processing Systems, vol. 25, 2012.

[11]

S Surjanovic and D Bingham, “Virtual Library of Simulation Experiments: Test Functions and Datasets,” sfu.ca. [Online]. Available: https://www.sfu.ca/~ssurjano/optimization.html. [Accessed March 11, 2023].

[12]

N Srinivas, A Krause, S M Kakade, and M Seeger, “Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design,” Proceedings of the 27th International Conference on Machine Learning, p. 1015-1022, 2010.

[13] (1,2)

CKI Williams, and CE Rasmussen, Gaussian Processes for Machine Learning, 2nd ed. Cambridge, MA: MIT press, 2006.

[14]

J Wilson, F Hutter, and M Deisenroth, “Maximizing Acquisition Functions for Bayesian Optimization,” Advances in Neural Information Processing Systems, vol. 31, 2018.

[15]

C Zhu, RH Byrd, P Lu, J Nocedal, “Algorithm 778: L-BFGS-B: Fortran Subroutines for Large-Scale Bound-Constrained Optimization,” ACM Transactions on Mathematical Software (TOMS), vol. 23, no. 4, p. 550-560, 1997.